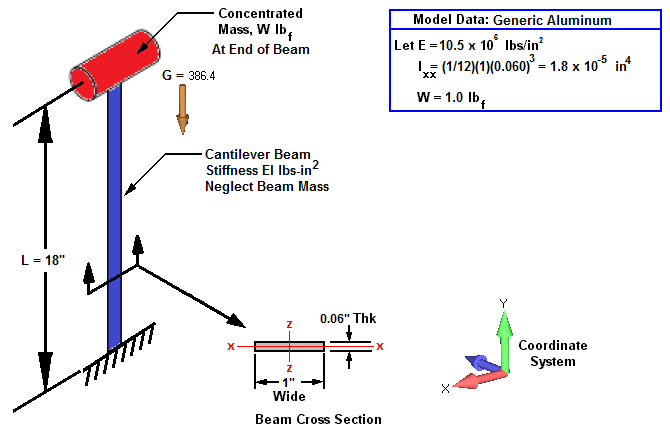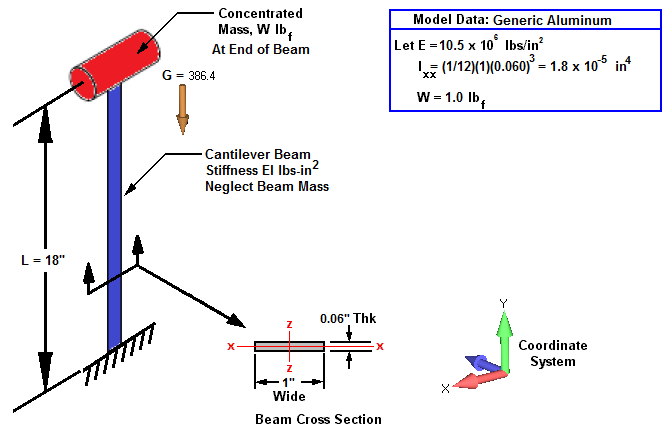
Fig. 1: Some resonant vibration frequencies for Cantilever beam with gravity.
August 1, 2014
By David Dearth
In this technical article, our topic is how to ensure correct resonant vibration frequencies are obtained when the structural stiffness of an assembly is very flexible and effects of gravity cannot be neglected.
Introduction
When performing resonant vibration analyses, one problem novice FEA (finite element analysis) analysts confront is how to ensure they have performed all the necessary tasks to generate the correct frequency solution. The answer to this question can be answered by taking the time to do sample problems. These sample FEA problems should be such that you can estimate a known theoretical solution. With a sample problem analysts can have a detailed hand sanity check that is completed using a pencil, paper and a calculator. If analysts cannot solve the same simple problems using a computer that can be completed using hand calculations then how they be confident in being able to solve their real problems using a computer?
When performing resonant vibration analysis most often analysts need only be concerned with stiffness, k, and mass, m. However when a structural system is quite flexible, it becomes necessary to also consider gravity forces acting upon the mass. Examples of flexible structural assemblies where the effects of gravity cannot be neglected when performing resonant vibrational analysis are scaffolding and conveyor systems.
Resonant Vibrations Review When External Loading is Present
Consider a simple pendulum system positioned in three different orientations with respect to gravity. A first order approximation to the natural frequency of a pendulum treated as a weightless cantilever beam with moment of inertia, I, and Young’s modulus, E, and a concentrated mass, m, attached to the free end is the following:
The gravitational term “g/l” is additive for a hanging pendulum and subtracts when the pendulum is inverted.
In finite element terms, this type of analysis is called “pre-stiffened modal analysis”.
Sample Problem: Resonant Vibration Frequencies with Gravity Included
For the cantilever beam system shown in the Fig. 1, assume the beam length is L=18 inches and the beam cross section is a rectangular section b = 0.06 inches x h=1.0 inches. The beam is assumed massless and a single concentrated weight, W= 1 lbf, attached to the free end of the beam.
Determine the resonant vibration frequencies of oscillation about the static equilibrium position in terms of Hz with and without the presence of gravity loading for three orientations with respect to gravity (a.) Horizontal, (b.) Vertical Up and (c.) Vertical Down.
FEA analysts should also solve this simple problem with a pencil, paper and a calculator. The perspective to keep in focus is that the same steps that analysts must jump through to solve this simple spring-mass system are the same steps needed to solve the real problem using the computer. The only difference between the FEA approach and the hand solutions are usually the complexity of the geometry.
| Orientation | Hand Solution | FEA Solution | Percent Difference |
|---|---|---|---|
| Horizonal | .0975487 Hz | 0.975481 Hz | -0.0006% |
| Vertical “Up” | 0.638606 Hz | 0.541560 Hz | -15.196% (1.) |
| Vertical “Down” | 1.222838 Hz | 1.264562 Hz | +3.412% |
Table 1: Summary Results — Resonant Vibration Frequencies with Gravity
Answers
When solving the differential equations of motion for the model shown with the beam mass neglected, the first order solutions to the decimal places of accuracy are fhoriz = 0.975 Hz, fUp = 0.639 Hz and fDwn = 1.223 Hz. Table 1, lists a comparison of summary results when an FEA model idealization of Fig. 1 is processed using MSC/Nastran and carrying both the exact and the numerical solution out to 6 decimal places of accuracy. Table 1 shows that for flexible systems gravity effects cannot be neglected otherwise FEA models for resonant frequency calculations will not be correct.
Notes: (1.) The large percentage difference between the theoretical hand solution and the FEA solution for the Vertical “Up” case may be due to the W=1 lb concentrated mass being close to the critical buckling load Pcr = 1.439 lbs. When the critical buckling load is reached or exceeded then the frequency becomes zero.
Documentation: Hand Calculations, Run Notes for FEA Models
Hand Calculations contains the detailed calculations and summary arithmetic.
Run Notes includes the keystroke summary for the FEA model shown in Fig. 1 in MSC/Nastran format.
Additional References:
Raymond J. Roark and Warren C. Young, “Formulas for Stress and Strain”, Chapter 15, Dynamic and Temperature Stresses, Table 36, Case 3, McGraw-Hill Book Company, 1975.
Dr. J. William Jones , Dr. Robert E. Nickell, William Bulat, “The Effects of Gravity on Structural Vibration”, Proceedings of the ASME Pressure Vessels and Piping Conference July 14-18, 2013,Paris, France PVP 2013-97571
David Dearth, P.E., is with Applied Analysis & Technology, Inc, Huntington Beach, CA. Contact him via [email protected].
Subscribe to our FREE magazine, FREE email newsletters or both!