Latest News
February 2, 2009
By Fred C. Jensen
« Page 1 |2
Reference 1, chapter 6.6.3, titled “Resistance Variational Methods,” explains this in one of the better treatments of this subject. The software developer lists five variational methods that can be used to simplify the fluid flow-pressure drop problem for complex mechanical assemblies. These methods, according to the reference, include Constant Loss Coefficients, Free Area Ratio, Friction Factor, Head Capacity or pressure-flow rate curve, and finally Permeability Coefficient or the Darcy equation.
We used a head-capacity curve to represent the complex mechanical component in each of our examples. Table 1 shows the pressure-flow relations for the HE as taken directly from Catacel Corp. test data. Table 2 shows the head capacity curve used in the second example for the reactor as taken from the historical data that was given in Reference 2, Figure 14-6, titled “The heat balance for the Shippingport PWR steam plant.”
So let’s pull out our toolbox, break down these two problems, and show how easy these become to solve. We will draw on the SolidWorks CAD program to build fluid models and the computational fluid dynamic program CFdesign from Blue Ridge Numerics for the actual CFD analysis.
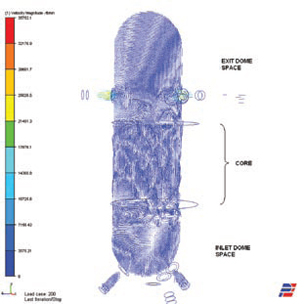 This a velocity vector plot of the nuclear reactor vessel. Note that only the space inside the inlet and exit domes shows the correct velocity. The velocity shown through the reactor core reflects the input headcapacity curve values. The values shown here reflect Table 2’s example input and not actualoperational data. |
The method described here does have some limitations. Since we are not modeling the actual cross-sectional flow areas inside the complex mechanical assemblies, the color plots of the velocity profiles will not show the true velocity values within the core. As seen in our examples, the core areas for the HE and the reactor are a uniform color at a low value. Also actual heat transfer cannot be modeled in the core areas. If the heat were modeled, resulting in a temperature change in the core, the gases would have to expand and the flow would be different from the input head capacity curve. One could account for heat transfer by altering the original resistance variational method chosen.
The described method has some very powerful pluses. First, multiple inlets and outlets can be applied as in our example of the nuclear reactor where all of the redundant primary coolant loop flows are included. Second, multiple complex mechanical assemblies in a pressure drop loop can be modeled as in the case of the primary coolant valves located in line with the reactor. Third, the velocity profile is reported correctly in the inlet and exit areas before and after the core. Finally, the pressure profiles show correctly along the entire color plot.
References:
1.) “CFdesign User’s Guide,” Version 8.0, Blue Ridge Numerics, Inc., 1992-2005.
2.) “Power Plant Theory and Design,” 2nd Edition, by Philip J. Potter, The Ronald Press Company, 1959.
3.) Catacel Corp., 7998 Gotham Road, Garrettsville, Ohio 44231, 2007-2008 test data.
More Info:
Catacel Corp.
Garrettsville, OH
CFdesign
Blue Ridge Numerics
Patriot Engineering Company
Chagrin Falls, OH
SolidWorks Corporation
Concord, MA
Fred C. Jensen is director of engineering at Patriot Engineering Co. Send your feedback to [email protected].
« Page 1 |2
Subscribe to our FREE magazine, FREE email newsletters or both!
Latest News
About the Author
DE’s editors contribute news and new product announcements to Digital Engineering.
Press releases may be sent to them via [email protected].